[알고리즘] 프림 알고리즘(Prim Algorithm)이란?
- Computer Science/[알고리즘]
- 2022. 10. 11.
프림 알고리즘(Prim`s Algorithm)이란?
프림 알고리즘은 크루스칼 알고리즘과 더불어 최소 신장 트리를 찾는 대표적인 알고리즘 중 하나이다. 크루스칼 알고리즘과 최소 신장 트리에 대해 잘 모른다면 이전 게시물을 보고 오자.
참고)
[알고리즘] 크루스칼 알고리즘(Kruskal Algorithm)이란? 크루스칼 알고리즘 C++ 구현, 최소 신장 트리(Mi
최소 신장 트리(Minimum Spanning Tree)란? 크루스칼 알고리즘에 대해 알아보기 위해선 우선 최소 신장 트리에 대해 알아야 한다. 우선, 신장 트리(Spanning Tree)란 무방향(Undirected) 그래프의 최소 연결 부
code-lab1.tistory.com
프림 알고리즘 과정
프림 알고리즘의 과정은 아래와 같이 간단한 편이다.
1. 임의의 정점을 선택해 서브 그래프 집합 T에 포함시킨다.
2. T에 속한 정점들과 T에 인접한 정점들 중 가장 가중치가 낮은 간선과 연결된 정점을 T에 포함시킨다.
3. 모든 정점이 포함될 때까지 2를 반복하면 T는 최소 신장 트리가 된다.
예시를 보며 이해하자. 아래와 같은 그래프가 있다고 하자.
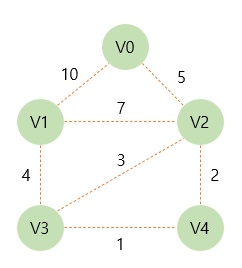
위 그래프에서 임의의 정점을 아무거나 선택하면 된다. 최소 신장 트리는 모든 정점을 포함해야하기 때문에 어떤 정점이든 무조건 연결되기 때문에 어떤 정점을 시작점으로 잡든지 상관없는 것이다.
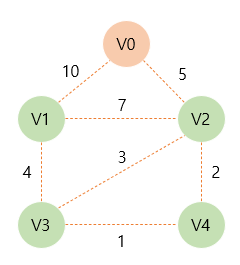
V0를 시작점으로 잡자. 이 때 V0는 T에 속하게 된다. 이후 T에 인접한 정점들 중 가장 가중치가 적은 간선으로 연결된 정점을 찾으면, V2가 5로 가장 작다.
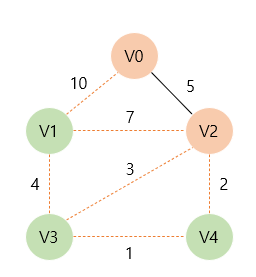
따라서 V2와 간선을 T에 포함시킨다. 이후 T에 인접한 정점들 중 가장 가중치가 적은 간선으로 연결된 정점을 찾으면, V4가 2로 가장 작다.
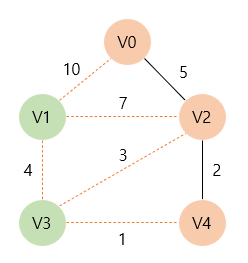
따라서 V4와 간선을 T에 포함시킨다. 이후 T에 인접한 정점들 중 가장 가중치가 적은 간선으로 연결된 정점을 찾으면, V3가 1로 가장 작다.
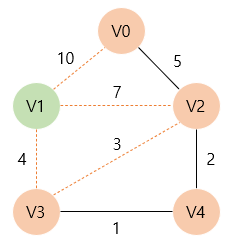
따라서 V3와 간선을 T에 포함시킨다. 이후 T에 인접한 정점들 중 가장 가중치가 적은 간선으로 연결된 정점을 찾으면, V1이 4로 가장 작다.
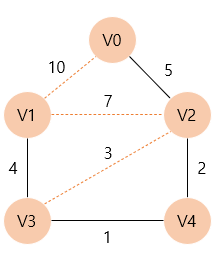
따라서 V1과 간선을 T에 포함시킨다. 모든 정점이 T에 포함되었으므로 과정을 종료한다.
이렇게 하면 T는 최소 신장 트리가 된다.
프림 알고리즘 시간 복잡도
프림 알고리즘의 핵심은 T에 속한 정점과 T에 속하지 않은 정점들 중 가장 가중치가 낮은 간선을 빠르게 찾는 것이다. 이것은 최소 힙을 이용해 빠르게 탐색할 수 있다.
정점의 개수가 V개, 모든 간선의 개수가 E인 그래프에서 단순 배열을 이용하면 모든 정점에서 다른 모든 정점을 탐색하므로 시간 복잡도는 O(V^2)이다.
하지만 최소 힙을 이용하여 빠르게 탐색한다면, O(ElogV)에 가능하다. 모든 정점을 탐색할 때 최소 힙을 이용하면 O(VlogV)에 최소 가중치를 찾을 수 있다. 하지만 최악의 경우 힙을 조정하는 경우 O(ElogV)가 걸린다.
따라서 시간 복잡도는 O( (V+E)logV ) = O(ElogV)이다. ( E>V 이므로)
참고)
[자료구조]Max Heap, Min Heap, Heap 이란? | C언어 Heap 구현
힙(Heap)이란? 완전이진트리의 일종이다. 여러 값들 중 최댓값 혹은 최솟값을 빠르게 찾아내기 위한 자료구조이다. 힙은 중복된 값을 허용한다. Max Heap 은 가장 큰 값을 빠르게 찾기 위한 것이고 Mi
code-lab1.tistory.com
'Computer Science > [알고리즘]' 카테고리의 다른 글
| [알고리즘] KMP알고리즘이란? KMP 알고리즘 C++ 구현 (2) | 2023.03.22 |
|---|---|
| [알고리즘] 투 포인터 알고리즘(Two-Pointers Algorithm)이란? 백준 2003번 C++ 풀이 (2) | 2022.12.08 |
| [알고리즘] 크루스칼 알고리즘(Kruskal Algorithm)이란? 크루스칼 알고리즘 C++ 구현, 최소 신장 트리(Minimum Spanning Tree)란? (0) | 2022.10.09 |
| [알고리즘] 벨만 포드(Bellman-Ford) 알고리즘 | c++ 벨만포드 구현 (0) | 2021.09.13 |
| [알고리즘] 다익스트라(Dijkstra) 알고리즘이란? | c++ 다익스트라 구현 (2) | 2021.08.11 |