[알고리즘] 투 포인터 알고리즘(Two-Pointers Algorithm)이란? 백준 2003번 C++ 풀이

투 포인터 알고리즘(Two-Pointers Algorithm)이란?

투 포인터 알고리즘은 말 그대로 두 개의 포인터를 이용해 문제를 해결하는 알고리즘을 뜻한다. 보통 l(left), r(right)나 s(start), e(end) 같은 식으로 포인터의 이름을 붙인다. 

 

투 포인터 알고리즘을 설명하기 위해 하나의 알고리즘 문제를 소개하겠다.

 

https://www.acmicpc.net/problem/2003

2003번: 수들의 합 2

 

백준에서 풀어볼 수 있는 대표적인 투 포인터를 활용한 문제이다. 문제는 다음과 같다.

 

N개의 수로 된 수열 A[1], A[2], …, A[N] 이 있다. 이 수열의 i번째 수부터 j번째 수까지의 합 A[i] + A[i+1] + … + A[j-1] + A[j]가 M이 되는 경우의 수를 구하는 프로그램을 작성하시오.

- N(1 ≤ N ≤ 10,000), M(1 ≤ M ≤ 300,000,000)

 

이때 모든 경우의 수를 테스트 한다면 O(N^2)으로 시간제한을 넘기게 된다. 이때 활용할 수 있는 알고리즘이 투 포인터 알고리즘이다.

 

 

이 문제를 해결하기 위해 s(start), e(end) 포인터를 이용하겠다. 이때 항상 s<=e 를 만족하도록 하고 s는 현재 부분 배열의 시작을, e는 현재 부분 배열의 끝을 가리키는 역할을 한다. 현재 부분배열의 합 sum은 s부터 e-1까지의 합으로 나타내겠다.

s=e인 경우는 sum=0이라고 하자. 

 

알고리즘은 매우 간단하다.

 

1. sum >=M 혹은 e==N이면 sum에서 A[s]를 빼고 나서 s를 증가(s++)하고 
2. 그렇지 않다면 e를 증가(e++)시키고 sum에 A[e]를 더한다 
3. sum==M이면 count

 

이해가 잘 안된다면 자세한 과정을 살펴보면서 이해해보자.

 

 

[그림 1] 투 포인터 알고리즘 과정(1)

 

 

처음엔 s와 e모두 index 0을 가리킨다고 하자.

이때 s부터 e까지의 부분합(sum)은 0이다. 따라서 e를 증가시킨다(e 포인터를 오른쪽으로 옮긴다고 생각하자)

 

 

[그림 2] 투 포인터 알고리즘 과정(2)

 

sum<M 이면 e는 계속 증가한다.

그러다 sum >=M이 되면 s를 증가시킨다(s 포인터를 오른쪽으로 옮긴다고 생각)

 

[그림 3] 투 포인터 알고리즘 과정(3)

 

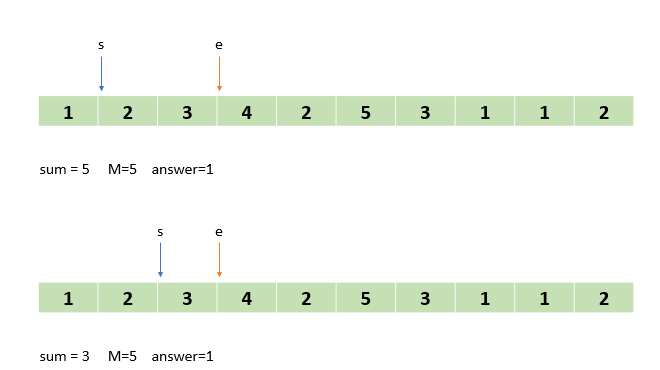
sum==M이 되면 정답을 count 해주고 또다시 s를 증가시켜준다.

 

[그림 4] 투 포인터 알고리즘 과정(4)

 

 

계속 같은 과정을 반복해준다.

 

 

[그림 5] 투 포인터 알고리즘 과정(5)

 

중간에 sum==M 인 경우가 있다면 count 해주고 계속 같은 과정을 반복한다.

 

[그림 6] 투 포인터 알고리즘 과정(6)

 

중간에 sum==M 인 경우가 있다면 count 해주고 계속 같은 과정을 반복한다. e==N 이 됐다면 계속해서 s를 증가시켜준다.

 

[그림 7] 투 포인터 알고리즘 과정(7)

 

s가 배열의 끝에 다다르면 과정을 종료한다. 이렇게 정답 3을 찾아내는 과정이 완료되었다.

 

 

이처럼 투 포인터 알고리즘을 사용하면 O(N) 시간 복잡도로 문제를 해결할 수 있다. 어떻게 O(N)이 될까? s와 e는 매 과정에서 무조건 1씩 증가하게 된다. s와 e는 최대 N까지 증가할 수 있으며 항상 s<=e 이기 때문에 둘이 증가하는 과정은 최대 N번만 반복될 것이다. 따라서 투 포인터 알고리즘을 사용하면 O(N^2) 걸리는 문제를 O(N)에 해결할 수 있다.

 

 

하지만, 투 포인터 알고리즘이 모든 정답을 찾아내는가에 대해 의문을 가질 수 있다. 이것에 대해서는 아래와 같이 증명할 수 있다.

 

[그림 8] 투 포인터 알고리즘 증명

 

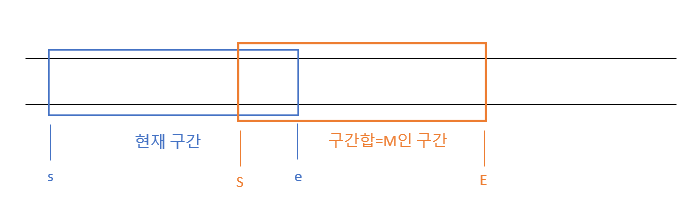
S부터 E까지의 구간합이 M인 구간이 있다고 하자. 우리는 이 구간이 몇 개 있는지 찾아야한다. 이때 투 포인터 알고리즘을 사용하면 저 구간을 놓칠 수 없다. 만약 저 구간을 놓치는 상황을 가정해보자.

 

 

1. s=S 가 되기전에 e가 E를 넘어가는 경우

[그림 9] e가 E를 넘어가는 경우(1)

 

[그림 9]와 같이 s가 S가 되기 전에 e가 E를 넘어가는 경우가 존재할 수 있을까? 이런 경우는 발생할 수 없다.

 

 

[그림 10] e가 E를 넘어가는 경우(2)

 

s와 e는 한 칸씩 오른쪽으로 이동한다. 이때 e는 무조건 E를 한 번은 지나가게 되는데, 만약 s가 S보다 왼쪽에 있다면, s부터 e까지의 구간합은 무조건 M보다 클 수밖에 없다(물론 이것은 배열이 모두 자연수라는 가정하에서다. 배열에 음수가 있다면 성립하지 않는다). 따라서 이경우 e가 오른쪽으로 이동하는 일은 절대 발생할 수 없다.

 

2. e가 E가 되기전에 s가 S를 넘어가는 경우

 

이 경우와 1과 마찬가지로 증명할 수 있으므로 생략하겠다. e가 E가 되기 전에 s는 절대 S를 넘어갈 수 없다.

 

 

따라서 우리는 투 포인터 알고리즘을 이용해 모든 경우의 수를 셀 수 있다.

 

 

풀이

 

#include <iostream>
using namespace std;
 
int main(){
    int N, M, arr[10000];
    cin >> N >> M;
    for(int i=0; i<N; i++){
        cin >> arr[i];
    }
        
    int answer = 0, sum = 0, s = 0, e = 0;
    while(s<N){
        if(sum >= M){ 
            sum -= arr[s];
            s++;
        }else{
            sum += arr[e];
            e++;
        } 
        if(sum == M) answer++;
    }
    
    cout << answer;
}

 

 

 

 

 

 

 

---

참고

 

1. https://m.blog.naver.com/kks227/220795165570