최소 신장 트리(Minimum Spanning Tree)란?
크루스칼 알고리즘에 대해 알아보기 위해선 우선 최소 신장 트리에 대해 알아야 한다.
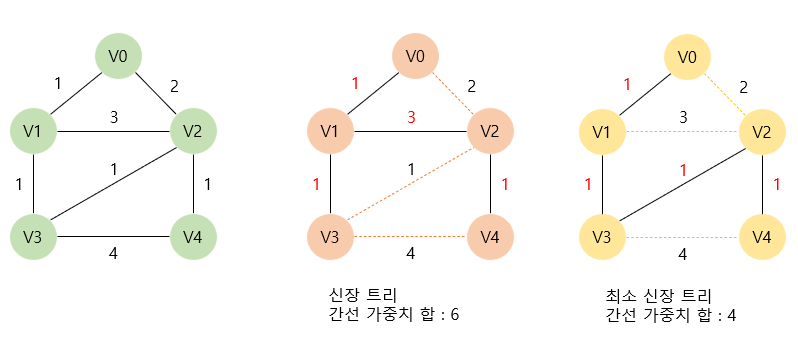
우선, 신장 트리(Spanning Tree)란 무방향(Undirected) 그래프의 최소 연결 부분 그래프이다. 좀 더 쉽게 설명하자면 N개의 정점을 가지는 그래프 중 최소 간선의 수인 N-1개의 간선으로 연결된 그래프를 뜻한다. N개의 정점이 N-1개의 간선으로 연결되어 있으면 이것은 필연적으로 트리 형태를 이루게 되기 때문에 신장 트리라고 불린다.
[그림 1]을 보면 5개의 정점을 가진 그래프를 4개의 간선만을 사용해 연결하면 신장 트리가 되는 것을 볼 수 있다. 신장 트리는 하나의 그래프에서 여러 개가 나올 수 있다.
최소 신장 트리는 이러한 신장 트리들 중 간선의 가중치 합이 가장 작은 트리를 뜻한다. [그림 1]의 가장 오른쪽 신장 트리가 최소 신장 트리가 된다.
크루스칼 알고리즘에 대해 알기 위해서는 그래프에 대한 기본적인 개념과 용어를 알아햐 하기 때문에 해당 개념을 잘 모른다면 다음을 참고하자.
참고)
[자료구조] 그래프(Graph)의 개념과 이해, 용어 | 인접행렬 vs 인접리스트 그래프 구현
그래프란? 그래프는 연결되어 있는 원소 사이의 다대다 관계를 표현하는 자료구조이다. 그래프 G는 객체를 나타내는 정점 V(vertex)와 객체를 연결하는 간선 E(edge)의 집합이다. 트리도 그래프의 한
code-lab1.tistory.com
크루스칼 알고리즘(Kruskal`s Algorithm)이란?
크루스칼 알고리즘은 그리디 알고리즘(Greedy Algorithm)의 일종으로 최소 신장 트리를 구하는 대표적인 알고리즘 중 하나이다.
크루스칼 알고리즘은 다음과 같은 과정을 거친다.
1. 간선의 가중치를 오름차순으로 정렬한다.
2. 오름차순으로 정렬된 간선들을 탐색하며 해당 간선을 신장 트리에 포함할 때
2-1) 사이클이 발생한 경우 신장 트리에 포함하지 않고 넘어간다.
2-2) 사이클이 발생하지 않는 경우 신장 트리에 포함한다.
3. 모든 정점을 연결할 때까지 위 과정을 반복한다.
예를 들어 다음과 같은 그래프를 보자.
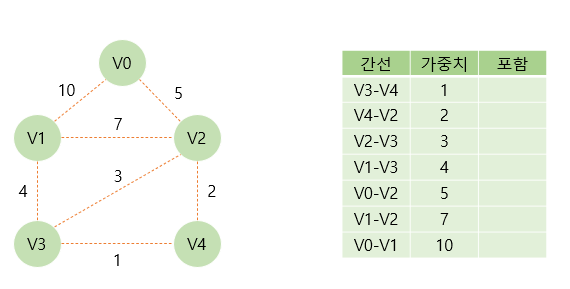
위와 같은 그래프가 있을 때, 가장 먼저 그래프의 간선들을 가중치의 오름차순으로 정렬한다. 이후 가중치가 작은 간선부터 신장 트리에 포함시킬지 여부를 사이클의 여부를 통해 결정한다.
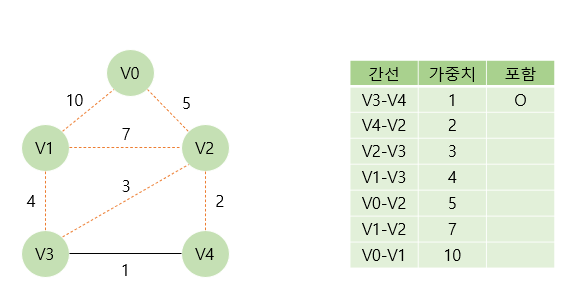
가장 먼저 V3와 V4를 연결하는 간선을 신장 트리에 포함시킬지 여부를 결정한다. 해당 간선을 포함해도 사이클이 발생하지 않으므로 포함시킨다.
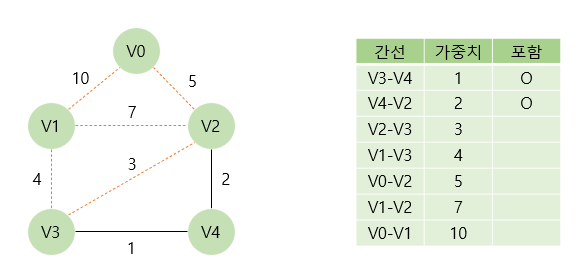
이후 V2와 V4를 연결하는 간선을 신장 트리에 포함시킬지 여부를 결정한다. 해당 간선을 포함해도 사이클이 발생하지 않으므로 포함시킨다.
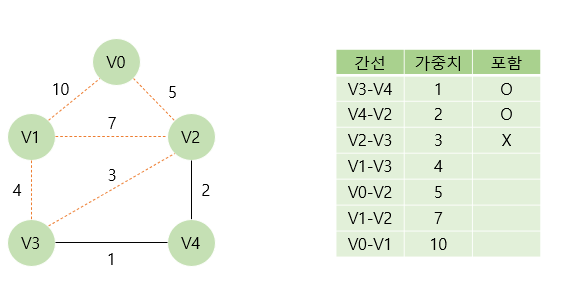
이후 V2와 V3를 연결하는 간선을 신장 트리에 포함시킬지 여부를 결정한다. 해당 간선을 포함하면 사이클이 발생하기 때문에 포함시키지 않는다.
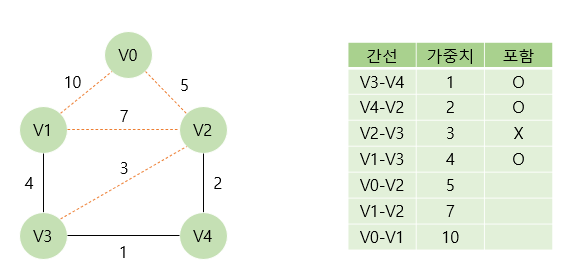
이후 V1와 V3를 연결하는 간선을 신장 트리에 포함시킬지 여부를 결정한다. 해당 간선을 포함해도 사이클이 발생하지 않으므로 포함시킨다.
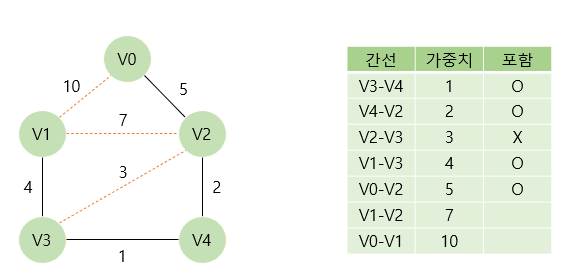
이후 V2와 V0를 연결하는 간선을 신장 트리에 포함시킬지 여부를 결정한다. 해당 간선을 포함해도 사이클이 발생하지 않으므로 포함시킨다. 이때 모든 정점이 연결되었으므로 더 이상 탐색을 진행하지 않고 과정을 종료한다.
이렇게 하면 모든 정점을 연결한 다음과 같은 최소 신장 트리를 구하게 된다.
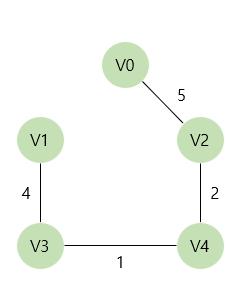
이런 최소 신장 트리를 구하는 알고리즘은 어떻게 활용할 수 있을까? 예를 들어 여러 개의 도시를 연결하는 도로를 건설한다고 하자. 간선의 가중치를 도로를 건설하는 비용이라고 했을 때, 모든 도시를 연결할 때 가장 비용을 줄일 수 있는 방법을 크루스칼 알고리즘을 통해 해결할 수 있다.
크루스칼 알고리즘 C++ 구현
크루스칼 알고리즘을 구현하기 위해서는 union-find 알고리즘에 대해 알아야한다. 해당 알고리즘에 대해 잘 모른다면 다음을 참고하자. (필자도 추후 포스팅 예정)
참고)
유니온 파인드(Union-Find)
유니온 파인드란? 유니온 파인드는 그래프 알고리즘으로 두 노드가 같은 그래프에 속하는지 판별하는 알고리즘이다. 서로소 집합, 상호 베타적 집합(Disjoint-Set)으로도 불린다. 노드를 합치는 Unio
ip99202.github.io
크루스칼 알고리즘 C++ 구현은 다음 코드를 참고하자. 해당 코드를 변형하여 적용시킬 수 있다.
#include <stdio.h>
#include <vector>
#include <algorithm>
using namespace std;
int parent[5]; //노드 연결용, 연결노드가 바뀌는지 체크
class Edge{
public:
int node[2];
int distance;
Edge(int a, int b, int distance){
this->node[0] = a;
this->node[1] = b;
this->distance = distance;
}
//오름차순 정렬 기준
bool operator<(Edge &edge){
return this->distance < edge.distance;
}
};
// 부모 탐색
int findParent(int node){
if(parent[node]==node) return node;
return findParent(parent[node]);
}
//두 노드를 작은값을 기준으로 연
void unionParent(int node1, int node2){
node1 = findParent(node1);
node2 = findParent(node2);
if(node1<node2) parent[node2] = node1;
else parent[node1] = node2;
}
//싸이클이 존재하면 true, 아니면 false를 반환
bool isCycle(int node1, int node2){
node1 = findParent(node1);
node2 = findParent(node2);
if(node1==node2) return true;
else return false;
}
int main(){
//그래프 생
vector<Edge> v;
v.push_back(Edge(0, 1, 10));
v.push_back(Edge(0, 2, 5));
v.push_back(Edge(1, 2, 7));
v.push_back(Edge(1, 3, 4));
v.push_back(Edge(2, 3, 3));
v.push_back(Edge(2, 4, 2));
v.push_back(Edge(3, 4, 1));
//간선 가중치 기준 오름차순 정렬
sort(v.begin(), v.end());
//부모노드 초기화
for(int i=1; i<=5; i++){
parent[i] = i;
}
int sum = 0; // 간선의 가중치 합
for(int i=0;i<v.size();++i){
//싸이클 여부 확인
if(!isCycle(v[i].node[0], v[i].node[1])){
sum += v[i].distance;
unionParent(v[i].node[0], v[i].node[1]);
}
}
// 최소 신장 트리 가중치 합 출력
printf("%d\n", sum);
return 0;
}