피보나치 수열
피보나치수열은 제2항 까지는 1, 제3항부터는 바로 앞의 두 항을 더한 수가 반복되는 수열이다.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55...
이러한 피보나치수열을 구현할 때는 보통 재귀를 통해 표현하게 된다. c언어에서는 아래와 같이 구현 할 수 있다.
|
1
2
3
4
5
6
|
int fibo(int n){
if (n<=2)
return 1;
else
return fibo(n-1) + fibo(n-2);
}
|
cs |
이렇게 재귀를 통해 피보나치 수열을 구하게 되면 중복 연산이 많아져 매우 비효율적이다. 예를 들어 fibo(5)를 구한다고 하자.
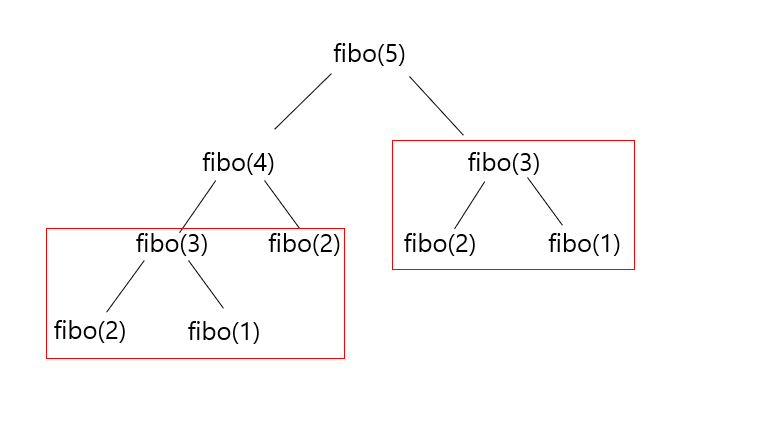
fibo(5)를 구할 때 위와 같은 과정을 거쳐 구하게 된다. 그림을 보면 fibo(1), fibo(2), fibo(3) 연산이 중복되는 것을 볼 수 있다. 만약 fibo(1), fibo(2), fibo(3) 연산의 값을 어딘가에 저장해 놓는다면, 중복해서 연산하지 않아도 될 것이다.
동적 계획법(Dynamic Programming)
동적 계획법은 복잡한 문제를 여러 개의 간단한 문제(하위 문제)로 나누어 풀고, 그것을 결합하여 최종적인 문제를 해결하는 것이다. 이때 각 하위 문제들의 답을 저장해놓고 같은 하위 문제가 나타난다면 미리 구한 답을 이용하면 된다. 분할 정복(Divide and Conquer) 방식과 비슷하지만 분할 정복은 하위 문제가 중복되지 않는다는 점이 다르다.
메모이제이션(Memoization)
동일한 문제를 반복해야 할 경우, 미리 계산해서 저장해 둔 결과를 활용하여 중복 연산을 줄이는 방식을 메모이제이션이라고 한다. 동적 계획법은 중복되는 하위 문제를 메모이제이션을 이용해 효율적으로 해결할 수 있다.
동적 계획법을 이용한 피보나치수열 해결
동적 계획법은 Top-down 방식과 Bottom-up 방식 두 가지 접근법이 존재한다. 이를 피보나치수열을 예로 들어서 fibo(n)을 구하는 방식을 두 가지로 나누어보자.
1. Top-down 방식
1) 큰 문제를 작은 문제(하위 문제)로 나눈다.
2) 작은 문제(하위 문제)를 푼다.
3) 작은 문제의 답을 결합해 최종 문제를 해결한다.
피보나치수열을 예로 들자면 아래와 같은 과정을 거치게 된다.
1) 큰 문제를 작은 문제(하위 문제)로 나눈다.
- fibo(n-1)과 fibo(n-2) 로 문제를 나눈다.
2) 작은 문제(하위 문제)를 푼다.
- fibo(n-1) 과 fibo(n-2)를 구한다. 이때 이미 구한 값이라면 저장한 값을 이용한다. 구해놓지 않은 값이라면 이를 메모이제이션 배열에 저장해 놓는다.
3) 작은 문제의 답을 결합해 최종 문제를 해결한다.
- fibo(n-1)과 fibo(n-2) 값을 더해 fibo(n)을 구한다.
c언어로 이를 구현하면 아래와 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
#include <stdio.h>
int dp[100] = {0,}; // 하위 문제 답을 저장할 메모이제이션 배열
int fibo(int n) {
if (n <= 1) {
return n;
} else {
if (dp[n] > 0) { // 해당 문제의 답이 존재
return dp[n];
}
dp[n] = fibo(n-1) + fibo(n-2);
return dp[n];
}
}
int main(){
printf("%d", fibo(5));
return 0;
}
|
cs |
이렇게 Top-down 방식으로 구현하면 메모이제이션의 장점을 제대로 활용할 수 없다. 연산 수가 줄어들어 기존의 방식보다는 효율적이지만 재귀적인 함수 호출로 인한 Overhead가 여전히 존재하므로 비효율적이다.
2. Bottom-up 방식
Bottom-up 방식은 작은 문제들부터 해결하여 이를 결합해 큰 문제를 해결하는 방식이다.
1) 작은 문제들부터 푼다.
2) 작은 문제들의 답을 이용해 큰 문제를 푼다.
3) 이를 반복해 최종 문제를 푼다.
피보나치수열을 예로 들자면 아래와 같은 과정을 거치게 된다.
1) 작은 문제들부터 푼다.
- fibo(i-1) , fibo(i-2) 값을 나타낼 dp [i-1] , dp [i-2]를 구한다.
2) 작은 문제들의 답을 이용해 큰 문제를 푼다.
- dp[i-1] + dp[i-2] 를 이용해 dp [i]를 구한다.
3) 이를 반복해 최종 문제를 푼다.
- 이를 반복해 dp [n]을 구한다.
c언어로 이를 구현하면 아래와 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
#include <stdio.h>
int dp[100] = {0,}; // 하위 문제 답을 저장할 메모이제이션 배열
int fibo(int n) {
dp[0] = 0;
dp[1] = 1;
int i;
for (i=2; i<=n; i++) { // 2부터 시작해서 n까지 반복
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
int main(){
printf("%d", fibo(5));
return 0;
}
|
cs |
이렇게 메모이제이션 배열을 이용해 bottom-up 방식으로 피보나치수열을 풀게 되면 재귀 함수 호출로 인한 overhead 가 없고, 연산 수도 줄어들어 효율적이다.
'Computer Science > [알고리즘]' 카테고리의 다른 글
| [알고리즘] 백트래킹(Backtracking) | C언어 N-Queen구현 (2) | 2021.07.27 |
|---|---|
| [알고리즘] 너비 우선 탐색(Breadth First Search : BFS) 이란? (0) | 2021.07.26 |
| [알고리즘] 깊이 우선 탐색, DFS(Depth First Search)알고리즘이란?| C언어 DFS 구현 (0) | 2021.07.26 |
| [알고리즘] 그리디(Greedy), 탐욕 알고리즘 | 거스름돈 문제 (0) | 2021.07.21 |
| [알고리즘] Divide and Conquer(분할정복)이란? | Merge Sort(병합정렬) (0) | 2021.07.09 |