최소 신장 트리(Minimum Spanning Tree)란?
크루스칼 알고리즘에 대해 알아보기 위해선 우선 최소 신장 트리에 대해 알아야 한다.
[caption id="attachment_414" align="alignnone" width="798"]
[그림1]
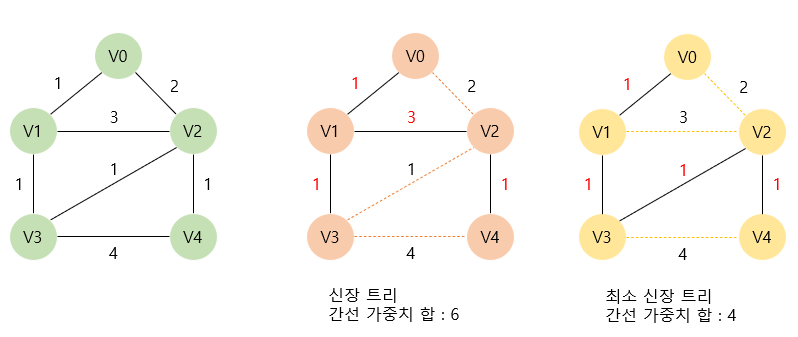
우선, 신장 트리(Spanning Tree)란 무방향(Undirected) 그래프의 최소 연결 부분 그래프이다. 좀 더 쉽게 설명하자면 N개의 정점을 가지는 그래프 중 최소 간선의 수인 N-1개의 간선으로 연결된 그래프를 뜻한다. N개의 정점이 N-1개의 간선으로 연결되어 있으면 이것은 필연적으로 트리 형태를 이루게 되기 때문에 신장 트리라고 불린다.
[그림 1]을 보면 5개의 정점을 가진 그래프를 4개의 간선만을 사용해 연결하면 신장 트리가 되는 것을 볼 수 있다. 신장 트리는 하나의 그래프에서 여러 개가 나올 수 있다.
최소 신장 트리는 이러한 신장 트리들 중 간선의 가중치 합이 가장 작은 트리를 뜻한다. [그림 1]의 가장 오른쪽 신장 트리가 최소 신장 트리가 된다.
크루스칼 알고리즘에 대해 알기 위해서는 그래프에 대한 기본적인 개념과 용어를 알아햐 하기 때문에 해당 개념을 잘 모른다면 다음을 참고하자.
[자료구조] 그래프(Graph)의 개념과 이해, 용어 , 인접행렬 vs 인접리스트 그래프 구현
그래프란?그래프는 연결되어 있는 원소 사이의 다대다 관계를 표현하는 자료구조이다.그래프 G는 객체를 나타내는 정점 V(vertex)와 객체를 연결하는 간선 E(edge)의 집합이다.트리도 그래프의 한
code-lab1.tistory.com
크루스칼 알고리즘(Kruskal`s Algorithm)이란?
크루스칼 알고리즘은 그리디 알고리즘(Greedy Algorithm)의 일종으로 최소 신장 트리를 구하는 대표적인 알고리즘 중 하나이다.
크루스칼 알고리즘은 다음과 같은 과정을 거친다.
1. 간선의 가중치를 오름차순으로 정렬한다.
2. 오름차순으로 정렬된 간선들을 탐색하며 해당 간선을 신장 트리에 포함할 때
2-1) 사이클이 발생한 경우 신장 트리에 포함하지 않고 넘어간다.
2-2) 사이클이 발생하지 않는 경우 신장 트리에 포함한다.
3. 모든 정점을 연결할 때까지 위 과정을 반복한다.
예를 들어 다음과 같은 그래프를 보자.

[그림 2]
위와 같은 그래프가 있을 때, 가장 먼저 그래프의 간선들을 가중치의 오름차순으로 정렬한다. 이후 가중치가 작은 간선부터 신장 트리에 포함시킬지 여부를 사이클의 여부를 통해 결정한다.

[그림 3]
가장 먼저 V3와 V4를 연결하는 간선을 신장 트리에 포함시킬지 여부를 결정한다. 해당 간선을 포함해도 사이클이 발생하지 않으므로 포함시킨다.

[그림 4]
이후 V2와 V4를 연결하는 간선을 신장 트리에 포함시킬지 여부를 결정한다. 해당 간선을 포함해도 사이클이 발생하지 않으므로 포함시킨다.

[그림 5]
이후 V2와 V3를 연결하는 간선을 신장 트리에 포함시킬지 여부를 결정한다. 해당 간선을 포함하면 사이클이 발생하기 때문에 포함시키지 않는다.

[그림 6]
이후 V1와 V3를 연결하는 간선을 신장 트리에 포함시킬지 여부를 결정한다. 해당 간선을 포함해도 사이클이 발생하지 않으므로 포함시킨다.

[그림 7]
이후 V2와 V0를 연결하는 간선을 신장 트리에 포함시킬지 여부를 결정한다. 해당 간선을 포함해도 사이클이 발생하지 않으므로 포함시킨다. 이때 모든 정점이 연결되었으므로 더 이상 탐색을 진행하지 않고 과정을 종료한다.
이렇게 하면 모든 정점을 연결한 다음과 같은 최소 신장 트리를 구하게 된다.

[그림 8]
이런 최소 신장 트리를 구하는 알고리즘은 어떻게 활용할 수 있을까? 예를 들어 여러 개의 도시를 연결하는 도로를 건설한다고 하자. 간선의 가중치를 도로를 건설하는 비용이라고 했을 때, 모든 도시를 연결할 때 가장 비용을 줄일 수 있는 방법을 크루스칼 알고리즘을 통해 해결할 수 있다.
크루스칼 알고리즘 C++ 구현
크루스칼 알고리즘을 구현하기 위해서는 union-find 알고리즘에 대해 알아야한다. 해당 알고리즘에 대해 잘 모른다면 다음을 참고하자. (필자도 추후 포스팅 예정)
https://ip99202.github.io/posts/%EC%9C%A0%EB%8B%88%EC%98%A8-%ED%8C%8C%EC%9D%B8%EB%93%9C(Union-Find)/
유니온 파인드(Union-Find)
유니온 파인드란? 유니온 파인드는 그래프 알고리즘으로 두 노드가 같은 그래프에 속하는지 판별하는 알고리즘이다. 서로소 집합, 상호 베타적 집합(Disjoint-Set)으로도 불린다. 노드를 합치는 Unio
ip99202.github.io
크루스칼 알고리즘 C++ 구현은 다음 코드를 참고하자. 해당 코드를 변형하여 적용시킬 수 있다.
#include <stdio.h>
#include <vector>
#include <algorithm>
using namespace std;
int parent[5]; //노드 연결용, 연결노드가 바뀌는지 체크
class Edge{
public:
int node[2];
int distance;
Edge(int a, int b, int distance){
this->node[0] = a;
this->node[1] = b;
this->distance = distance;
}
//오름차순 정렬 기준
bool operator<(Edge &edge){
return this->distance < edge.distance;
}
};
// 부모 탐색
int findParent(int node){
if(parent[node]==node) return node;
return findParent(parent[node]);
}
//두 노드를 작은값을 기준으로 연
void unionParent(int node1, int node2){
node1 = findParent(node1);
node2 = findParent(node2);
if(node1<node2) parent[node2] = node1;
else parent[node1] = node2;
}
//싸이클이 존재하면 true, 아니면 false를 반환
bool isCycle(int node1, int node2){
node1 = findParent(node1);
node2 = findParent(node2);
if(node1==node2) return true;
else return false;
}
int main(){
//그래프 생
vector<Edge> v;
v.push_back(Edge(0, 1, 10));
v.push_back(Edge(0, 2, 5));
v.push_back(Edge(1, 2, 7));
v.push_back(Edge(1, 3, 4));
v.push_back(Edge(2, 3, 3));
v.push_back(Edge(2, 4, 2));
v.push_back(Edge(3, 4, 1));
//간선 가중치 기준 오름차순 정렬
sort(v.begin(), v.end());
//부모노드 초기화
for(int i=1; i<=5; i++){
parent[i] = i;
}
int sum = 0; // 간선의 가중치 합
for(int i=0;i<v.size();++i){
//싸이클 여부 확인
if(!isCycle(v[i].node[0], v[i].node[1])){
sum += v[i].distance;
unionParent(v[i].node[0], v[i].node[1]);
}
}
// 최소 신장 트리 가중치 합 출력
printf("%d\n", sum);
return 0;
}
'Computer Science > [알고리즘]' 카테고리의 다른 글
| [알고리즘] 프림 알고리즘(Prim Algorithm)이란? (0) | 2025.04.24 |
|---|---|
| [알고리즘] 벨만 포드(Bellman-Ford) 알고리즘, 벨만포드 C++ 구현 (0) | 2025.04.24 |
| [알고리즘] 다익스트라(Dijkstra) 알고리즘이란? 다익스트라 c++ 구현 (0) | 2025.04.24 |
| [알고리즘] 백트래킹(Backtracking)이란? N-Queen C언어 구현 (0) | 2025.04.24 |
| [알고리즘] 너비 우선 탐색(BFS-Breadth First Search) 이란? (0) | 2025.04.24 |
